Testi on tarkoitettu kisallioppiminen.fi -sivuston MAB2-kurssin itsearviointiin.
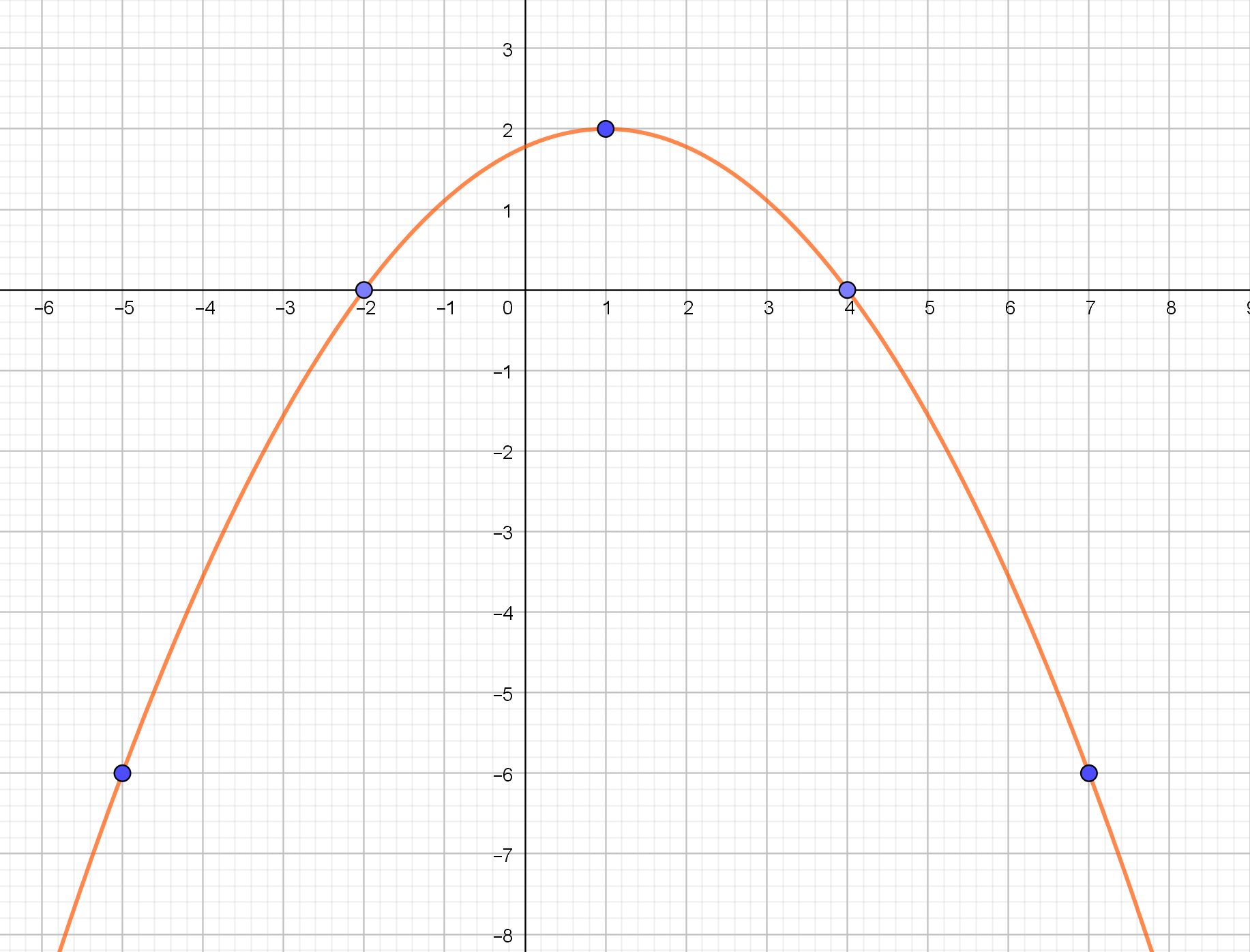
a) Toisen asteen polynomifunktion huippu on pisteessä (1,2) ja lisäksi kuvaajalla on pisteet (-2,0) ja (-5,-6). Hahmottele funktion kuvaaja.
b) Kerro, mitä kerroin $a$ ja kerroin $c$ kertovat toisen asteen polynomifunktion $f(x)=ax^2+bx+c$ kuvaajasta.
a) Kuvan pisteet oikein (2 p.)

Kuvaan hahmoteltu vapaalla kädellä paraabeli (1 p.)
b) Kerroin a kertoo, onko kyseessä ylös- vai alaspäin aukeava paraabeli. (1 p.) Jos a>0, niin kyseessä on ylöspäin aukeava paraabeli ja jos a<0, niin kyseessä on alaspäin aukeava paraabeli. (1 p.)
Kerroin c kertoo, millä korkeudella paraabeli leikkaa y-akselin. (1 p.)
a) Ratkaise yhtälö $x^2-9=0$ potenssiyhtälönä.
b) Ratkaise yhtälö $3x^2-12x=0$ tulon nollasäännön avulla.
c) Ratkaise yhtälö $2x^2-x=1$.
a) $x^2-9=0$
$x^2=9$ (1 p.)
$x=3$ tai $x=-3$ (1 p.)
b) $3x^2-12x=0$
$x(3x-12)=0$ (1 p.)
Tulon nollasäännön nojalla
$x=0$ tai $3x-12=0$ eli $x=4$. (1 p.)
c) Muokataan yhtälö muotoon, jossa toisella puolella on nolla.
$2x^2-x=1$
2x^2-x-1=0$
Poimitaan kertoimet a, b ja c.
a=2, b=-1 ja c=-1 (1 p.)
Toisen asteen yhtälön ratkaisukaavalla saadaan
\(x = {-(-1) \pm \sqrt{(-1)^2-4\cdot 2\cdot (-1)} \over 2\cdot 2}\)
\(x=\frac{1\pm\sqrt{9}}{4}\)
$x=\frac{1+3}{2}=\frac{4}{2}=2$ tai $x=\frac{1-3}{2}=\frac{-2}{2}=-1$. (1 p.)
Neliönmuotoista terassia laajennetaan toiseen suuntaan 2 metriä ja toiseen suuntaan 3 metriä. Tällöin terassin pinta-ala kaksinkertaistuu. Mikä oli alkuperäisen terassin sivun pituus?
Merkitään neliön sivun pituutta kirjaimella $x$. (1 p.)
Koska kyseessä on pituus, pitää olla $x>0$. (1 p.)
Suorakulmion pinta-ala lasketaan kaavalla kanta$\cdot$korkeus, joten uusi pinta-ala on $(x+2)\cdot (x+3)$. (1 p.)
Alkuperäinen pinta-ala on $x^2$.
Koska uusi pinta-ala on kaksinkertainen alkuperäiseen verrattuna, saadaan yhtälö
$(x+2)(x+3)=2x^2$ (1 p.) joka sievenee muotoon
$x^2+3x+2x+6-2x^2=0$
$-x^2+5x+6=0$ (1 p.)
Tämän ratkaisut saadaan toisen asteen yhtälön ratkaisukaavalla
$x=\frac{-5\pm{\sqrt{5^2-4\cdot(-1)\cdot6}}}{2\cdot(-1)}$
$x=\frac{-5\pm 7}{-2}$
$x=\frac{-5+7}{-2}=-1$ tai $x=\frac{-1-7}{-2}=6$.
Koska $x>0$, vain ratkaisu $x=6$ käy.
Vastaus: Terassin sivun pituus oli alun perin 6 metriä. (1 p.)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
